The Counting Balls (Example) 
Say we have a Room full of Red balls and Blue balls. We want to determine proportion of Red balls and Blue balls in that Room, But we can't count all the Balls in the Room there are too many of them.
So we took a small sample of balls from that room, and find the proportion of Red balls and Blue balls in that sample, and hope that proportion we just estimate is somewhat near the True proportion(for the whole room).
Remember that dogma we showed previously.
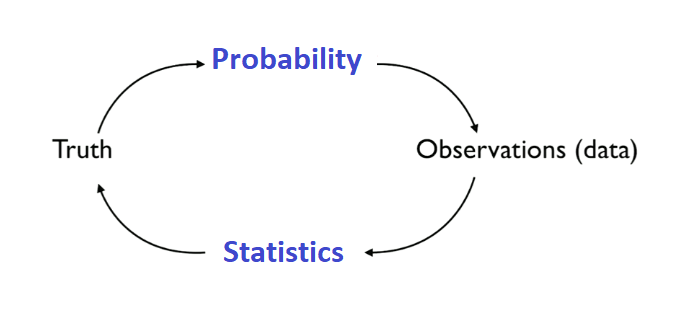
Truth
Let's first define the underlying truth, say that currently the Room is holding\(40\%\)
of Red Balls and \(60\%\)
of Blue Balls. Note that we do not know this proportion, our intent is to find this proportionSay we denote Red Balls by 1 and Blue Balls by 0
Probability
We use probability to generate our data using the Truth we defined above.Now let's create a Population in this case it's, all the balls in the Room.
(In this example we are creating
\(5000\)
Balls and \(40\%\)
of then are Red balls ) using Random
N = 5000
true_proportion_for_red = 0.40
n_red_balls = floor(Int, true_proportion_for_red*N)
population = zeros(Int8, (1,N))
population[1, 1:n_red_balls] = ones(Int8, (1, n_red_balls))
population = shuffle(population)
\(40\%\)
of Red Balls and \(60\%\)
of Blue Balls. Observation
As we can see Room is full of\(5000\)
Balls, and we can't count them all to find out the proportion of Red Balls and Blue Balls, so we took a sample out of those \(5000\)
balls, and then we find the proportion of Red Balls and Blue Balls in that small sample. So let's take a sample of
\(n=300\)
balls. n=300
sample = rand(population,n)
\(300\)
balls. These
\(300\)
observations (\(X_1,\cdots,X_{300}\)
) are what we call Random Variables. Statistics
So now we have our sample of\(300\)
balls, let's start finding an estimate for Red Balls proportion and Blue Balls proportion. To find the proportion of Red Balls we count number of Red Balls then we divide it by total number of balls (i.e.
\(300\)
). \(\hat{p}\)
: Our estimate for proportion of Red Balls denoted by \(1\)
. \(\hat{q}\)
: Our estimate for proportion of Blue Balls denoted by \(0\)
. \[ \hat{p} = \frac{1}{300}\sum_{i=0}^{300}X_i\]
\[ \hat{q} = 1-\hat{p} \]
p_hat = sum(sample)/n
q_hat = 1- p_hat
\(\hat{p}\)
).This is a single simulation if we perform this simulation multiple times we can get some insights for the distribution of our Random variable
\(\hat{p}\)
. Multiple simulations
using Plots, Random
gr(fmt = :png, size = (900, 500))
n_simulations = 1000 # Number of simulations
N = 5000 # population size
n = 300 # sample size
p = 0.40 # True proportion of red balls
estimators = Array{Float64}(undef, n_simulations) # Here we store estimates of every simulation
n_red_balls = floor(Int, p*N)
# population: all 5000 balls
population = zeros(Int8, (1,N))
population[1, 1:n_red_balls] = ones(Int8, (1, n_red_balls))
population = shuffle(population)
for i = 1:n_simulations
# extract sample from population
sample = rand(population,n)
estimators[i] = sum(sample)/n
end
Plots.xlabel!("Proportion of Red balls")
Plots.ylabel!("Counts")
Plots.histogram(estimators, label=false)
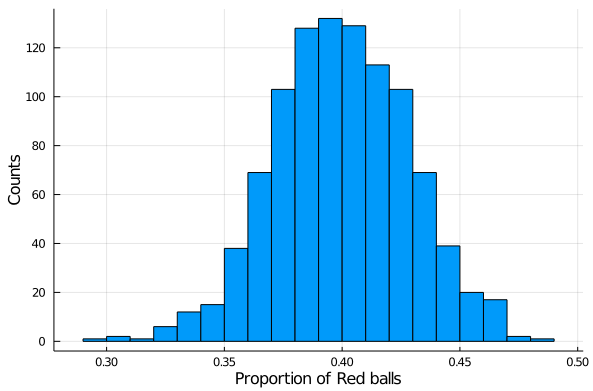
Does this (bell) curve seems familiar?
Simulation
Launch Statistics App


