Vector Space

Consider a vector

\vec{v}\in\mathbb{R}^d

, here

\vec{v}

lives in

\(d\)

dimensional space this space is a vector space.
For example for

\(d=3\)

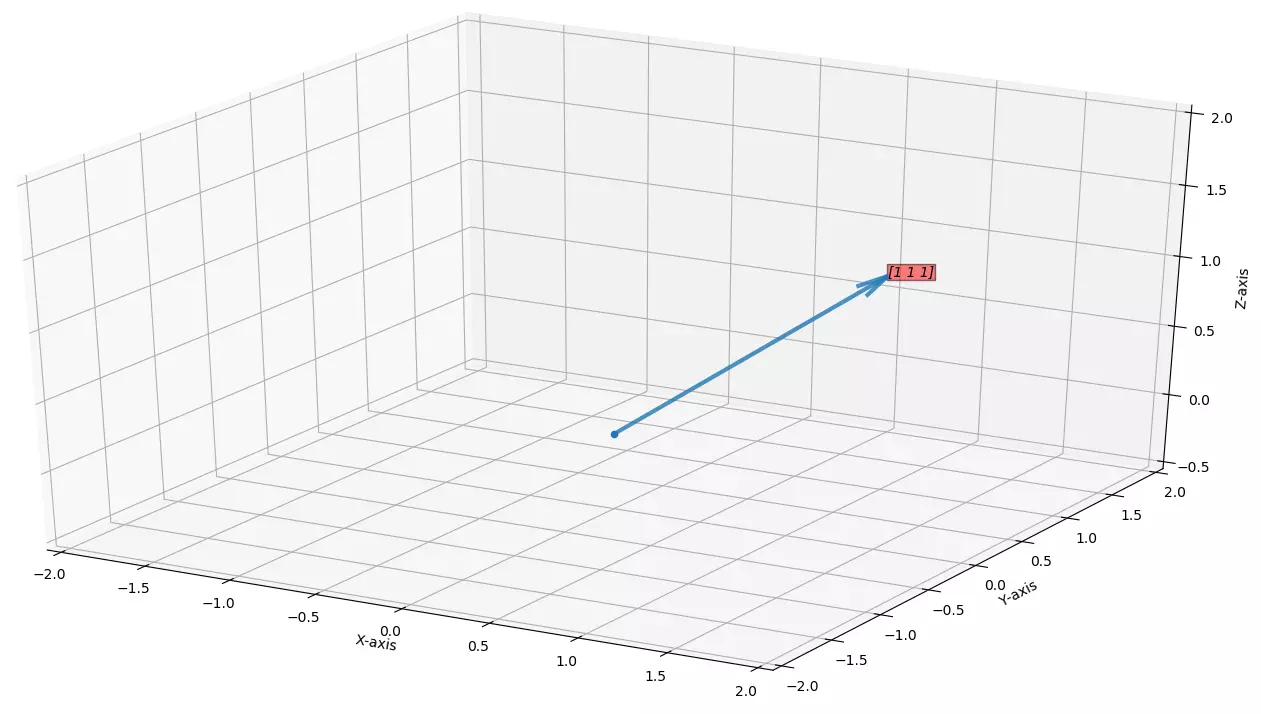
Vector shown in the blue is a vector

\vec{x}\in\mathbb{R}^3

. All the space surrounding this vector is

\(3\)

-dimensional vector space.

Code to plot this vector (python)

import MultiVariable as mvar
import numpy as np
%matplotlib qt
m = mvar.MultiVariable()
vector = np.array([[1,1,1]])
m.plot_3D_vectors(vector)
## Adjusting axis limits
m.set_axes_limit((-2,2))
m.setZ_limit((-0.5,2))

Download MultiVariable class

If we multiply a vector

\vec{v}

by a constant say

\(c\)

then the resulting vector is in direction of

\vec{v}

(or in opposite direction).
Say the resulting vector is

\vec{v}'

then we can say

\vec{v}' = c \vec{v}

where

c\in\mathbb{R}

, it is a line along vector

\vec{v}

.
Here you can see that

\vec{v}'

has it's own space inside that

\(d\)

dimensional space, it's a vector space inside a vector space.
Example for

\(d=3\)

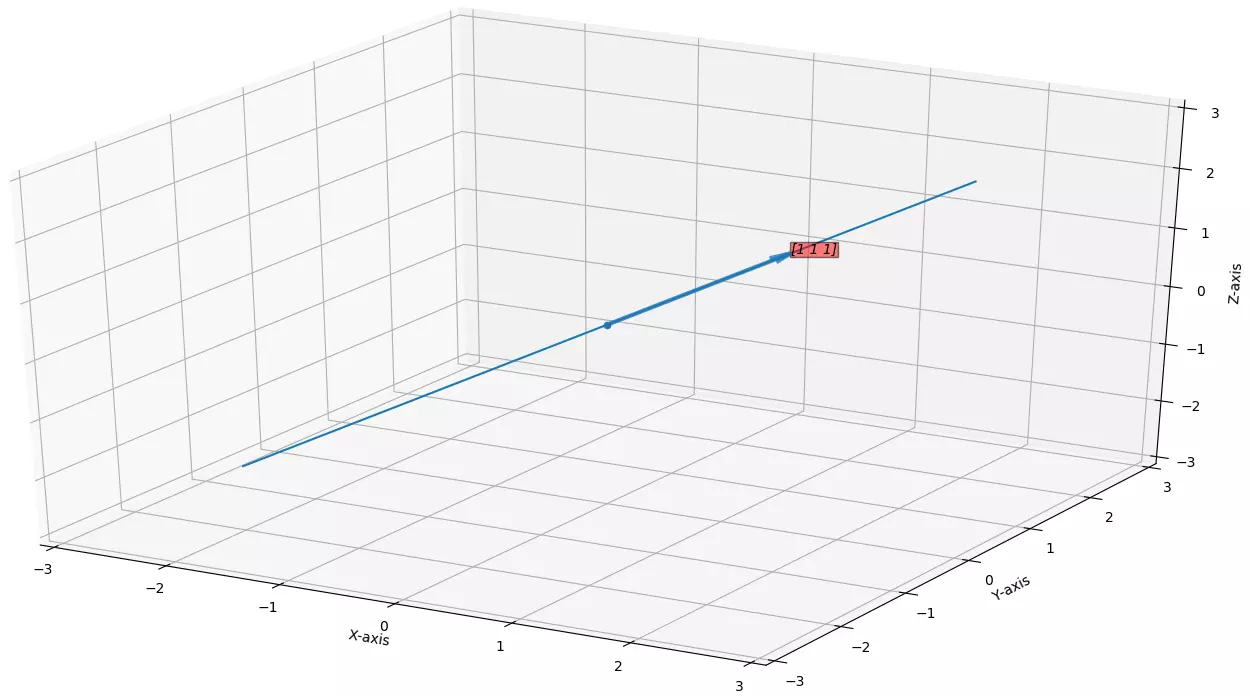
Here you can see the vector

\vec{x}\in\mathbb{R}^3

has it's own vector space that is that line.

Code To plot this vector (python)

import MultiVariable as mvar
import numpy as np
%matplotlib qt
m = mvar.MultiVariable()
## Here line is defines as [x-start, x-end, y-start, y-end, z-start, z-end]
lines = np.array([[-2,2,-2,2,-2,2]])
m.plot_3D_lines(lines)
vector = np.array([[1,1,1]])
m.plot_3D_vectors(vector, plot_separately=False)
## Adjusting axis limits
m.set_axes_limit((-3,3))

Download MultiVariable class

Now Consider a plane(passing through origin) inside a

\(3\)

-dimensional space, so that plane lives inside

\(3\)

-dimensional vector space, but it has it's own vector space.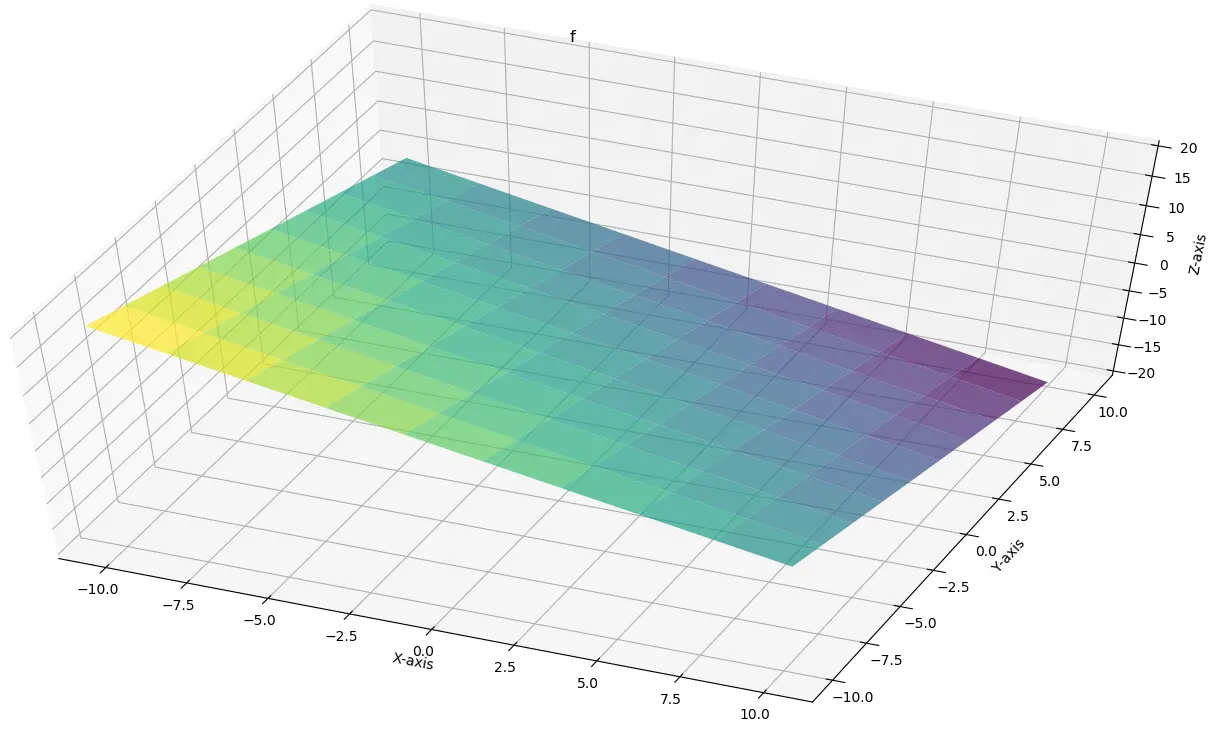

Code To plot this plane (python)

import MultiVariable as mvar
import numpy as np
%matplotlib qt

def f(x,y):
    return -x -y

m = mvar.MultiVariable()
m.plot_surface_color_3D(f, plot_separately=True, alpha=0.7)

Download MultiVariable class

Here you can see the plane

\(x+y+z=0\)

has it's own vector space inside

\(3\)

-dimensional vector space.

If we add any two

\(d\)

-dimensional vectors, we get a

\(d\)

-dimensional vector as a output.
Say we have two vectors

\vec{v}\in\mathbb{R}^d

and

\vec{w}\in\mathbb{R}^d

, then if we take there linear combination, then that linear combination will have it's own vector space, but what that vector space looks like?
Well it depends, on how

\vec{v}

and

\vec{w}

are oriented.
Case 1: if $\vec{v}$ is parallel to $\vec{w}$
If

\vec{v}

and

\vec{w}

are parallel then

\vec{w}= c \vec{v};\quad c\in\mathbb{R}

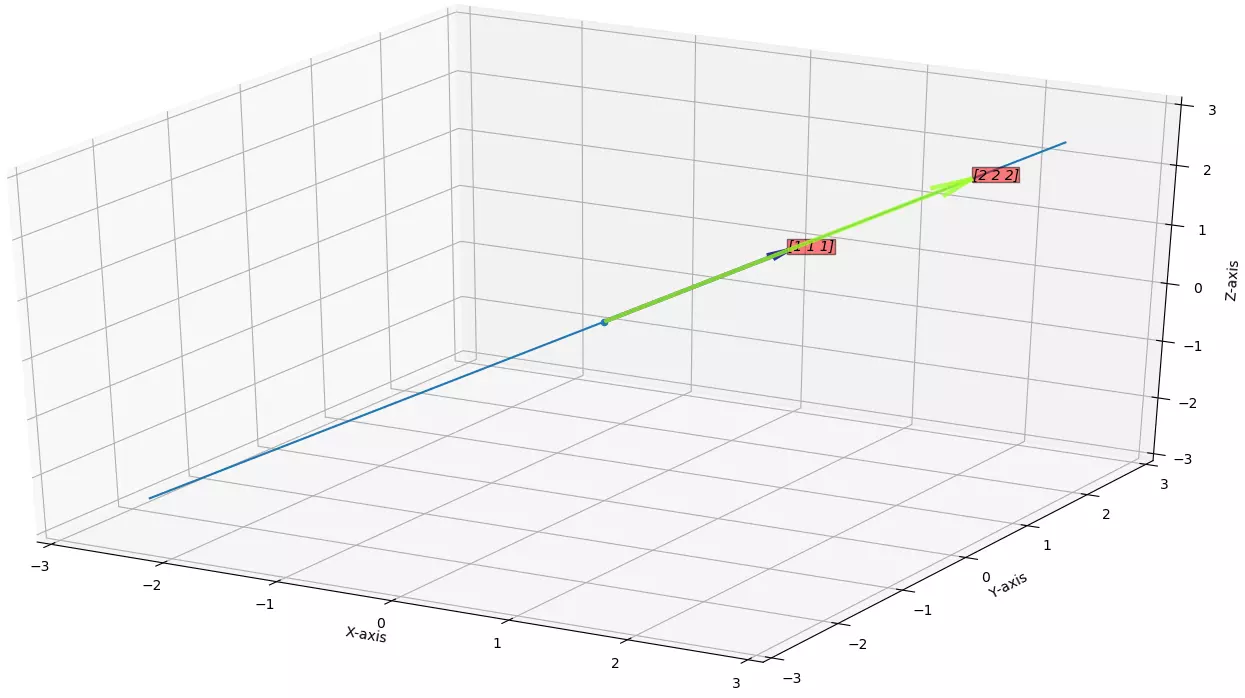
, So vector space is just a line.
Example for

\(d=3\)

:
Say the vectors are

\vec{v} = \begin{bmatrix} 1 \\ 1\\ 1\\ \end{bmatrix}

and

\vec{w} = \begin{bmatrix} 2 \\ 2\\ 2\\ \end{bmatrix}

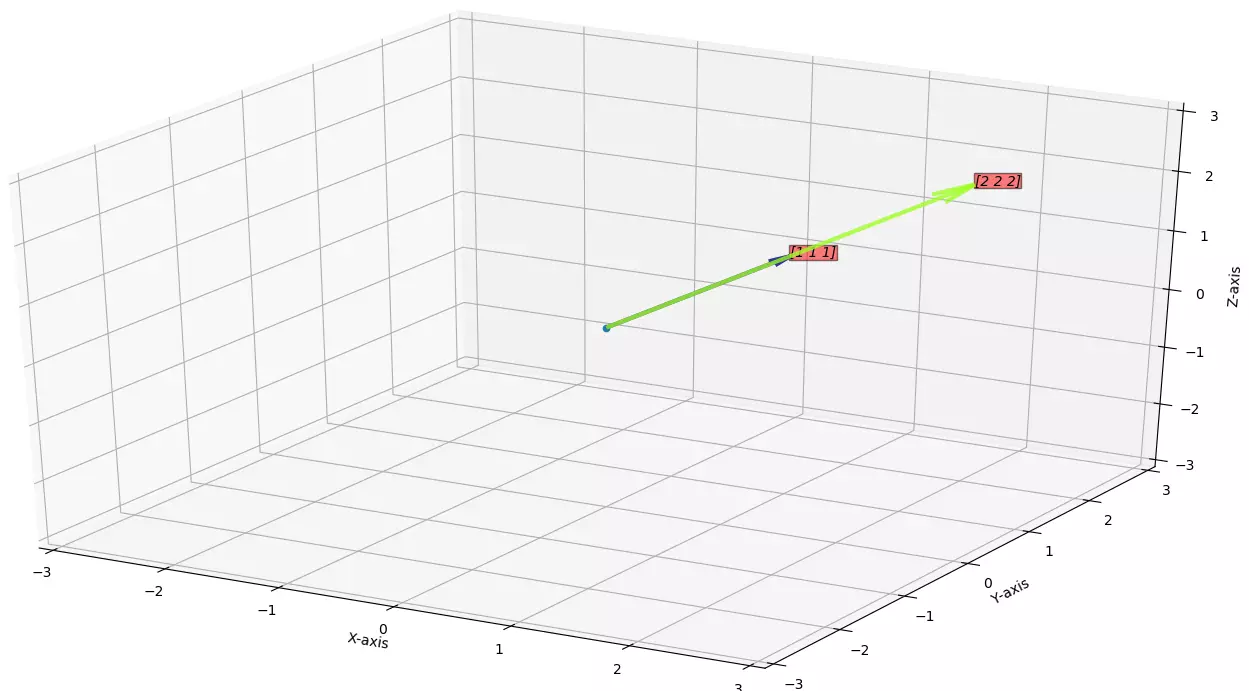
Then the vector space is just a line passing through these vectors.

Code To plot this (python)

import MultiVariable as mvar
import numpy as np
%matplotlib qt

m = mvar.MultiVariable()
vectors = np.array([
                    [1,1,1],
                    [2,2,2]
                   ])
origin = np.array([0,0,0])
m.plot_3D_vectors(vectors, origin, plot_separately=False)

# Structure of lines = [[x-start, x-end, y-start, y-end, z-start, z-end],...]
lines = np.array([[-2.5,2.5,-2.5,2.5,-2.5,2.5]])
m.plot_3D_lines(lines, plot_separately=False)
m.set_axes_limit((-3,3))

Download MultiVariable class

Case 2: if $\vec{v}$ is not parallel to $\vec{w}$
If

\vec{v}

and

\vec{w}

are not parallel then the vector space of linear combination of

\vec{v}

and

\vec{w}

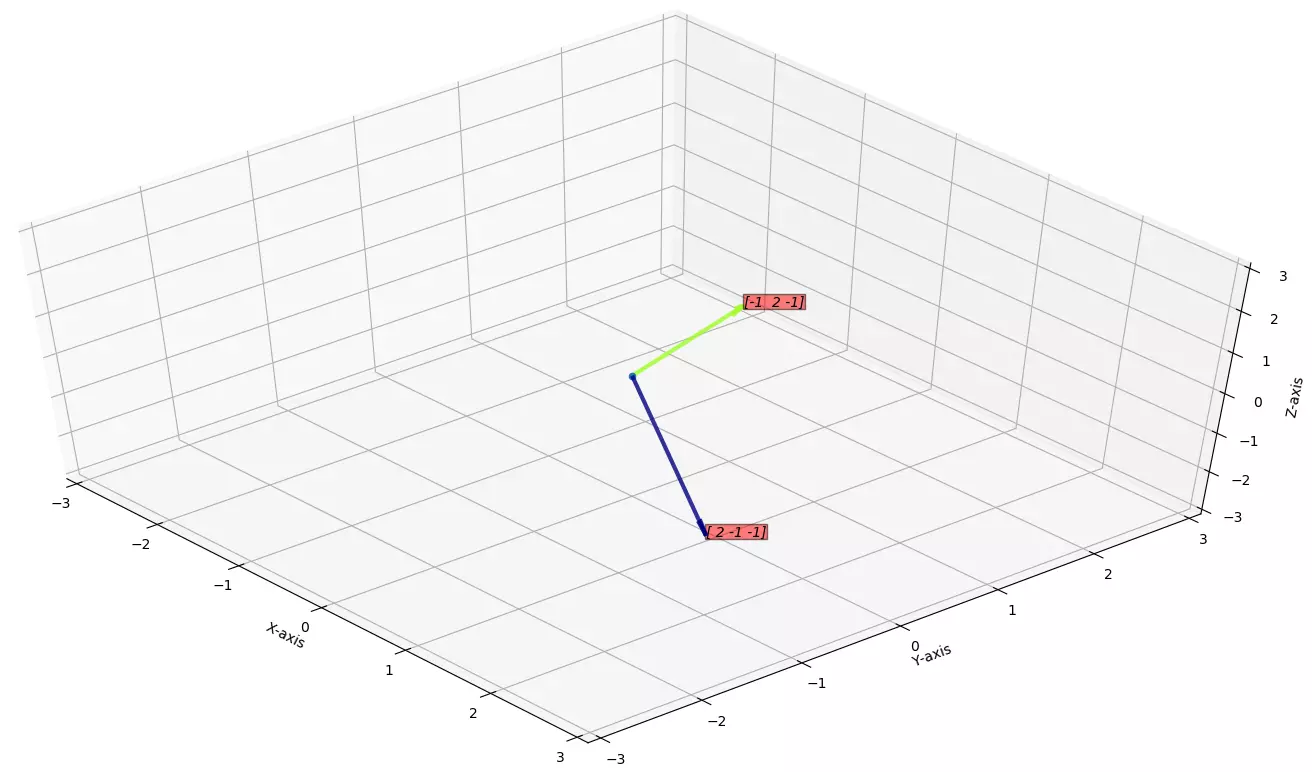
is a plane.
Example for

\(d=3\)

:
Say the vectors are

\vec{v} = \begin{bmatrix} 2 \\ -1\\ -1\\ \end{bmatrix}

and

\vec{w} = \begin{bmatrix} -1 \\ 2\\ -1\\ \end{bmatrix}

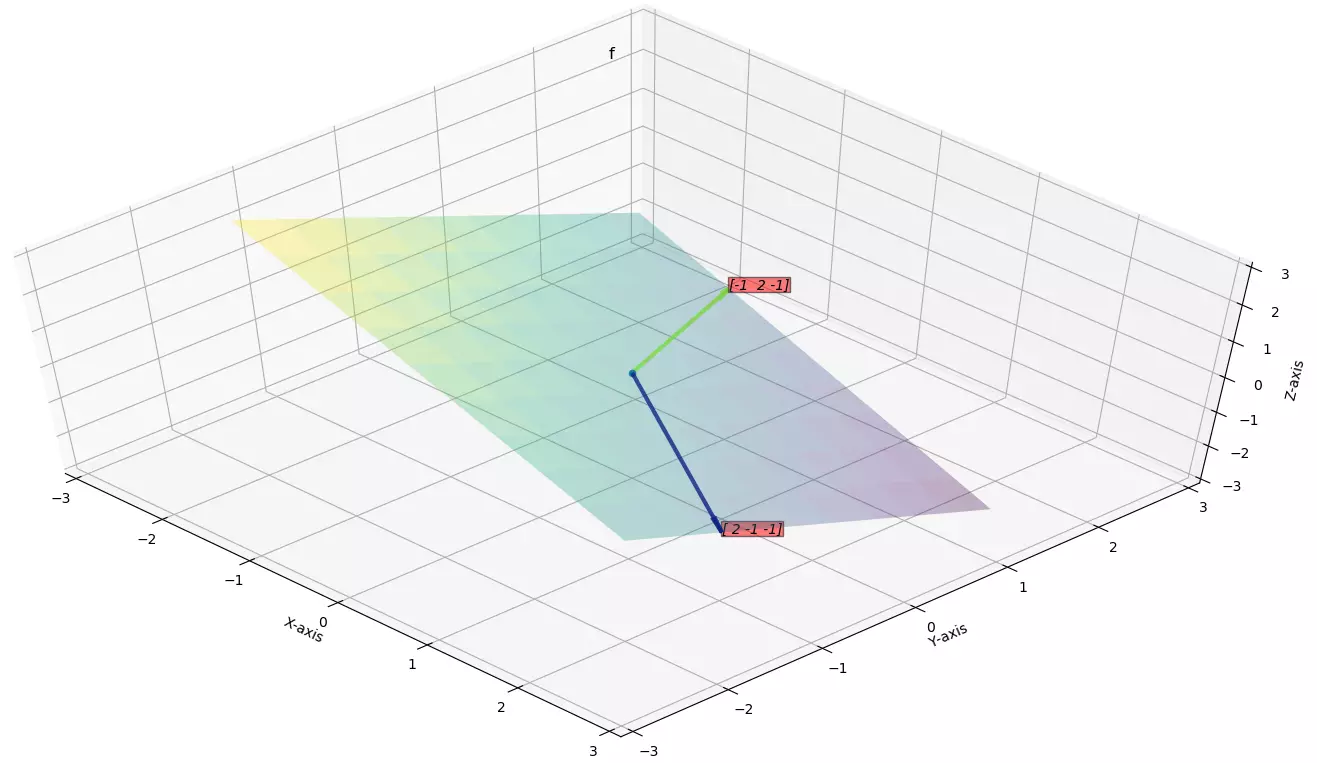
Then the vector space is the plane passing through these vectors.

Code To plot this (python)

import MultiVariable as mvar
import numpy as np
%matplotlib qt

# X + Y + Z = 0
def f(x,y):
    return -x -y

m = mvar.MultiVariable(count = 10, x_range=(-2,2), y_range=(-2,2), z_range=(-2,2))
vectors = np.array([
                    [2,-1,-1],
                    [-1,2,-1]
                   ])
origin = np.array([0,0,0])
m.plot_3D_vectors(vectors, origin, plot_separately=False)
m.plot_surface_lines_3d(f, density = 100, plot_separately=False)
m.set_axes_limit((-3,3))

Download MultiVariable class

Vector Space Properties

So when can we say that a space can be a vector space?
A space is a vector space if it full fill these conditions:

If there is a vector in that space and we multiply that vector with a constant $c\in\mathbb{R}$ then the resulting vector must be in the space
Say we took two vectors $\vec{v}$ and $\vec{w}$ then there sum must be in that space.

Let's see an example of a space which is not a vector space.
Think of a 2 dimensional space where

x\gt0

and

y\gt0

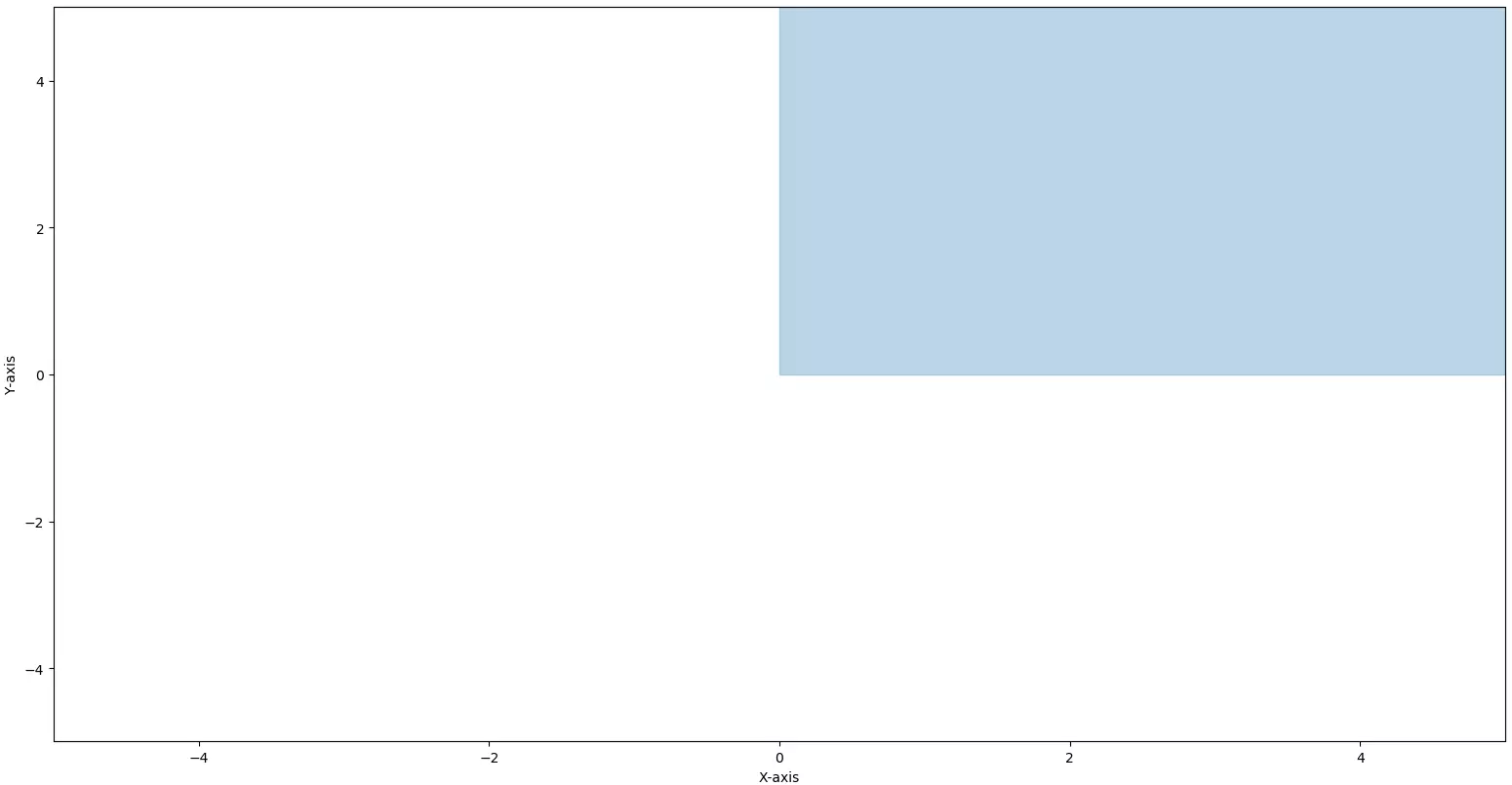
We can add vector safely and we don't go out of the space.
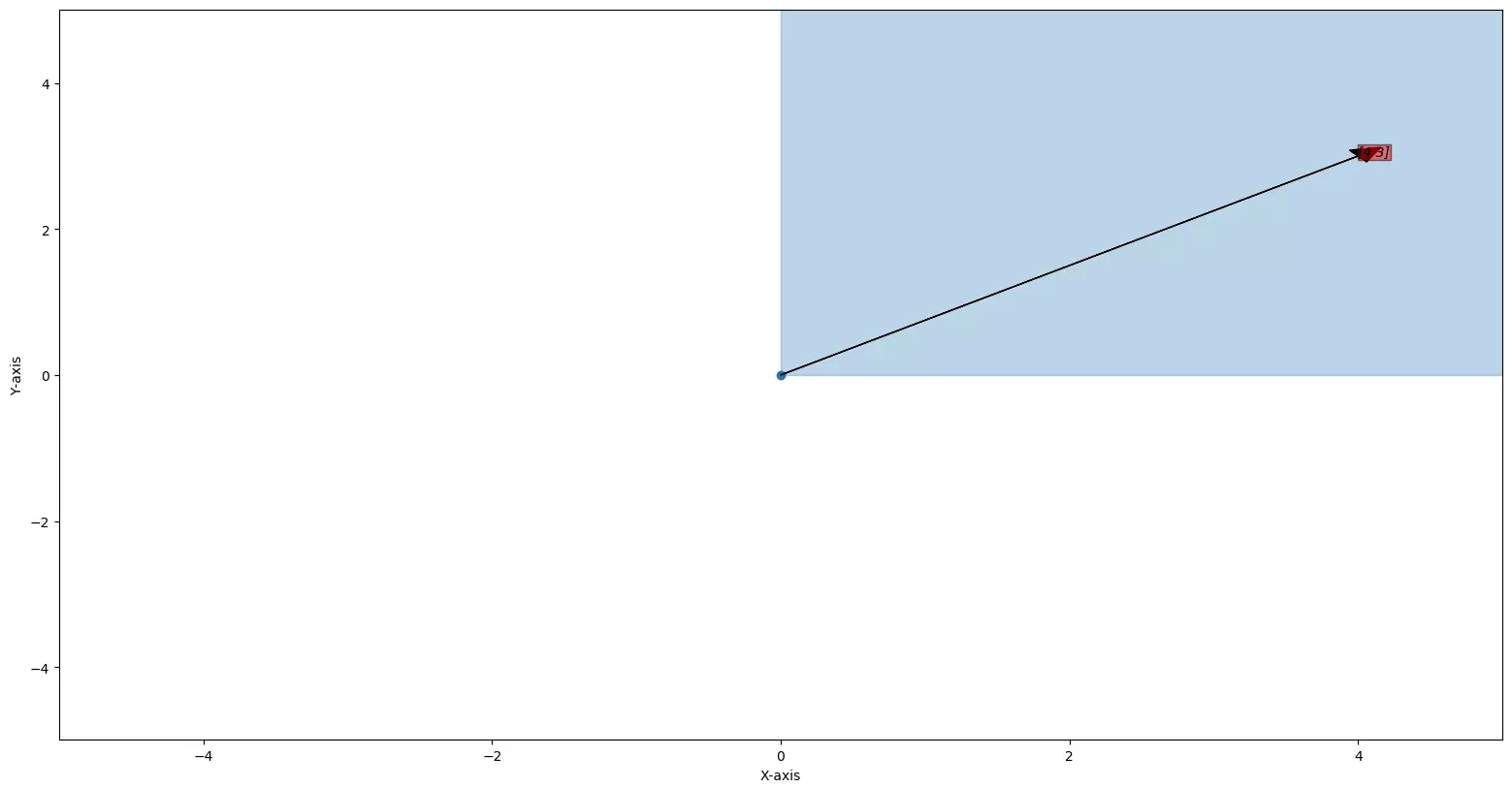
What about multiplying a constant to a vector, take a vector in that space

\vec{v}=\begin{bmatrix} 4 \\ 3\\ \end{bmatrix}

if we multiply

\vec{v}

\(-1\)

then if goes out of space.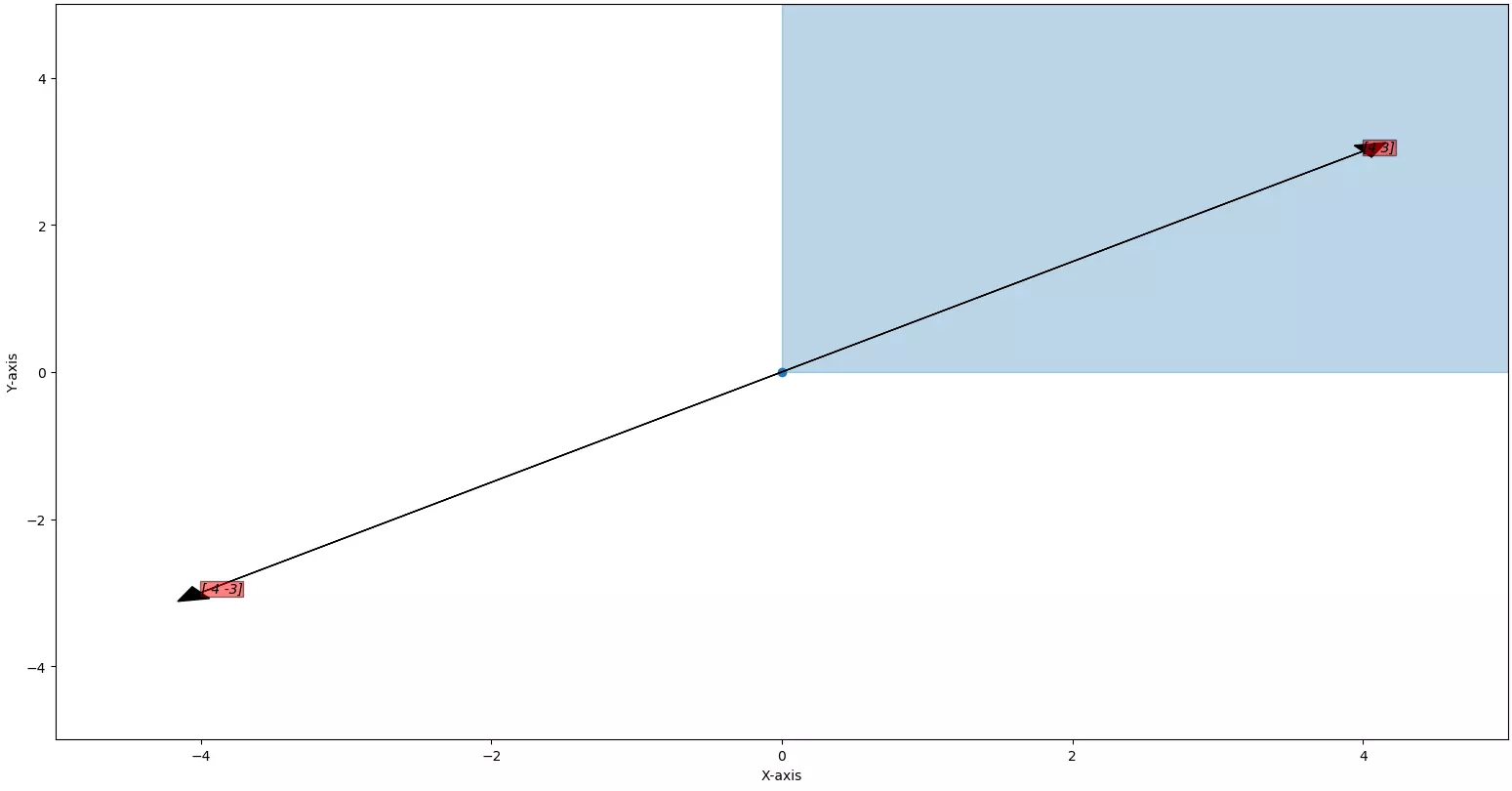

Code To plot this (python)

import MultiVariable as mvar
import numpy as np
%matplotlib qt

m = mvar.MultiVariable()

x = np.array([0,  5])
y1 = np.array([5,5])
y2 = np.array([0, 0])
m.fill_between(x, y1, y2, alpha=0.3)

vectors = np.array([
                    [4,3],
                    [-4,-3],
                   ])
origin = np.array([0,0])
m.plot_2D_vectors(vectors, origin, plot_separately=False, head_width=0.2, head_length=0.2)
m.set_axes_limit((-5,5))

Download MultiVariable class

So it can't be a vector space.

A vector space must pass through the origin.

Vector space inside a vector space is referred as a subspace.
Possible subspace of a

\(2\)

-dimensional space.

All $\mathbb{R}^2$ space
All lines passing through origin.
Origin itself( $\vec{0}$ )