Vector Projection

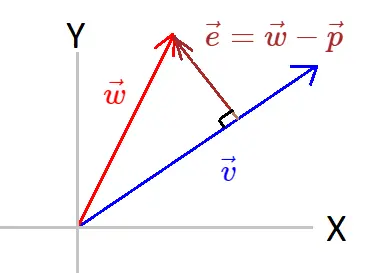Say that we have two vector

\vec{v}\in\mathbb{R}^2

and

\vec{u}\in\mathbb{R}^2

.
Now in space of $\vec{v}$ which vector is closest to

\vec{w}

?
But let's first ask what is the space of

\vec{v}

We are asking for the space of a single vector, a single vector can only give us a space in $\mathbb{R}$ which is a line.
So the span of $\vec{v}$ is $C\vec{v};\quad C\in\mathbb{R}$

Now we have to find a vector closest to

\vec{w}

in the vector space of

\vec{v}

.
Let's call this closest vector as

\vec{p}

, this

\vec{p}

is the projection of

\vec{w}

\vec{v}

.
We know that

\vec{p}

lives in the vector space of

\vec{v}

.
So

\vec{p}=x\vec{v};\quad x\in\mathbb{R}

\vec{p}

is the closest vector to

\vec{w}

then the vector joining

\vec{p}

\vec{w}

is perpendicular to

\vec{v}

.
Say the vector joining

\vec{p}

\vec{w}

\vec{e}

, and

\vec{e} = \vec{w}-\vec{p}

So,

$\vec{v}\cdot \vec{e} =0$
$\Rightarrow \vec{v}^T \vec{e} =0$
$\Rightarrow \vec{v}^T (\vec{w} -\vec{p})=0$
$\Rightarrow \vec{v}^T (\vec{w} -x\vec{v})=0$
$\Rightarrow \vec{v}^T \vec{w} -x\vec{v}^T\vec{v}=0$

\Rightarrow x=\frac{\vec{v}^T \vec{w}}{\vec{v}^T\vec{v}} \in\mathbb{R}

Projection of

\vec{w}

\vec{v}

\vec{p}=\vec{v}x

Projection Matrix of a vector

Say we have a vector

\vec{v}\in\mathbb{R}^n

now we want a matrix that gives us projection of any vector onto this vector

\vec{v}

, we call this matrix a projection matrix.
Say this projected vector on

\vec{v}

\vec{p}

.
As we discussed above,

\vec{p}=\vec{v}x

\displaystyle \Rightarrow \vec{p}= \vec{v} \frac{\vec{v}^T \vec{w}}{\vec{v}^T\vec{v}}

\displaystyle \Rightarrow \vec{p}= \frac{\vec{v} \vec{v}^T}{\vec{v}^T\vec{v}} \vec{w}

Projection matrix

\((P)\)

of a vector

\vec{v}

\begin{matrix} \displaystyle P=\frac{\vec{v}\ \vec{v}^T}{\vec{v}^T\vec{v}} \end{matrix}

Columns of

\(P\)

is the linear combinations of

\vec{v}

, so

Column space of $$P$$ is the vector space of $\vec{v}$ .

We have our Projection matrix

\((P)\)

we can take projection of any vector

\vec{w}

\vec{v}

by evaluating

P\vec{w}

In $P\vec{w}$ we are taking the linear combination of $\vec{v}$ so the resultant projection of $\vec{w}$ on $\vec{v}$ lives in the vector space of $\vec{v}$ .

What about the rank of

\(P\)

Rank of $$P$$ is $$1$$ .
Because all the columns of $$P$$ is the linear combination of a single vector $\vec{v}$ .

\(P\)

symmetric?

\displaystyle P= \frac{\vec{v} \vec{v}^T}{\vec{v}^T\vec{v}}

\displaystyle \Rightarrow P^T = \frac{(\vec{v} \vec{v}^T)^T}{\vec{v}^T\vec{v}}

\displaystyle \Rightarrow P^T = \frac{\vec{v}^{T^T} \vec{v}^T}{\vec{v}^T\vec{v}}

\displaystyle \Rightarrow P^T = \frac{\vec{v} \vec{v}^T}{\vec{v}^T\vec{v}}

\(P\)

is symmetric.

$\[P=P^T\]$

What if we apply the projection of a vector

\vec{w}

\vec{v}

twice?

When we apply the projection first time, we land in the vector space of

\vec{v}

.
Let's say the projected vector be

\vec{p}_1

.
If we again apply the projection on

\vec{p}_1

then it project the

\vec{p_1}

into the vector space of

\vec{v}

.
But

\vec{p}_1

is already in vector space of

\vec{v}

, so the second projection did nothing.
So we can say that

$\[P^2=P\]$

Why are we doing projection?

Ok we can find the projection of a vector on another vector, but why are we projecting the vector in the first place?
What is the benefit of projecting a vector?
Say a function

\(f=x_1 a+ x_2 b+ x_3 c\)

is governed by 3 variables (say

\(a,b,c\)

) and we have

\(5\)

noisy observation of

\(f\)

now we want to predict

\(f\)

for some set of

\((a,b,c)\)

.
Because our

\(5\)

observations are noisy so we can not perfectly predict the outcome.
Our observation is something like,

\(f_1=x_1 a_1+ x_2 b_1+ x_3 c_1\)

\(f_2=x_1 a_2+ x_2 b_2+ x_3 c_2\)

\(f_3=x_1 a_3+ x_2 b_3+ x_3 c_3\)

\(f_4=x_1 a_4+ x_2 b_4+ x_3 c_4\)

\(f_5=x_1 a_5+ x_2 b_5+ x_3 c_5\)

We can write it as,

\begin{bmatrix} a_1 & b_1 & c_1\\ a_2 & b_2 & c_2\\ a_3 & b_3 & c_3\\ a_4 & b_4 & c_4\\ a_5 & b_5 & c_5\\ \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3\\ \end{bmatrix} = \begin{bmatrix} f_1\\ f_2\\ f_3\\ f_4\\ f_5\\ \end{bmatrix}

Here

\(x_1 , x_2 , x_3\)

are our parameters(unknown), so our parameter space is

\mathbb{R}^5

.
We want to find a

\(4\)

dimensional plane that best fit our noisy data.
Say

\begin{bmatrix} a_1 \\ a_2 \\ a_3 \\ a_4 \\ a_5 \\ \end{bmatrix} = \vec{a},\quad

\begin{bmatrix} b_1 \\ b_2 \\ b_3 \\ b_4 \\ b_5 \\ \end{bmatrix} = \vec{b},\quad

\begin{bmatrix} c_1 \\ c_2 \\ c_3 \\ c_4 \\ c_5 \\ \end{bmatrix} = \vec{c},\quad

\begin{bmatrix} a_1 & b_1 & c_1\\ a_2 & b_2 & c_2\\ a_3 & b_3 & c_3\\ a_4 & b_4 & c_4\\ a_5 & b_5 & c_5\\ \end{bmatrix}= \mathbb{A}, \quad

\begin{bmatrix} x_1\\ x_2\\ x_3\\ \end{bmatrix}=\mathbb{X},\quad

and

\begin{bmatrix} f_1\\ f_2\\ f_3\\ f_4\\ f_5\\ \end{bmatrix} =\mathbb{Y}

\mathbb{A}\mathbb{X}=\mathbb{Y}

Our data is noisy.

\text{Rank}(\mathbb{A})\leq 3

\mathbb{X}\in\mathbb{R}^3

\mathbb{Y}\in\mathbb{R}^5

.
So there are high chance that

\mathbb{Y}

does not lives in column space of

\mathbb{A}

.
So instead we find the solution for

\mathbb{A}\widehat{\mathbb{X}}=\widehat{\mathbb{Y}}

.
Where

\widehat{\mathbb{Y}}

lives in the column space of

\mathbb{A}

and

\widehat{\mathbb{Y}}

is closest to

\mathbb{Y}

We can get this $\widehat{\mathbb{Y}}$ by taking the projection of $\mathbb{Y}$ onto the column space of $\mathbb{A}$

Matrix Projection

Say that we have a

m\times n

matrix

\mathbb{A}\in\mathbb{R}^{m\times n}

and a vector

\vec{v}\in\mathbb{R}^n

.
Then projection of a vector

\vec{v}

on a matrix

\mathbb{A}

generally means projection of

\vec{v}

on the column space of matrix

\mathbb{A}

.
We can also take the projection of a vector

\vec{v}

on the null space of matrix

\mathbb{A}^T

.
And as we know that null space of

\mathbb{A}^T

is perpendicular to the column space of

\mathbb{A}

.
Then,

Projection of a vector $\vec{v}$ on the,
null space of matrix $\mathbb{A}^T$ , and
column space of matrix $\mathbb{A}$
collectively gives us back our vector $\vec{v}$

Projection onto the column space of a matrix

Recall our previous example, here we have a system of equation

\mathbb{A}\mathbb{X}=\mathbb{Y}

where there is no solution.
Here problem was that there are high chance that

\mathbb{Y}

does not lives in column space of

\mathbb{A}

, So it does not have a solution.
So we go for the closest solution.

\mathbb{A}\widehat{\mathbb{X}}=\widehat{\mathbb{Y}}

where,

\widehat{\mathbb{Y}}

lives in the column space of

\mathbb{A}

, so.

$\widehat{\mathbb{Y}}$ is the linear combinations of the columns of $\mathbb{A}$ .

(vector)

\widehat{\mathbb{Y}}

lives in the column space

\mathbb{A}

and (vector)

\mathbb{Y}

is at some angle to the column space of

\mathbb{A}

, So

The vector $\mathbb{Y} - \widehat{\mathbb{Y}}$ is perpendicular to the column space of $\mathbb{A}$

\Rightarrow \mathbb{Y} - \widehat{\mathbb{Y}}

is also perpendicular to the column vectors of

\mathbb{A}

\Rightarrow

\vec{a}^T (\mathbb{Y} - \widehat{\mathbb{Y}})=0

\vec{b}^T (\mathbb{Y} - \widehat{\mathbb{Y}})=0

and

\vec{c}^T (\mathbb{Y} - \widehat{\mathbb{Y}})=0

where

\vec{a},

\vec{b}

and

\vec{c}

are the column vector of

\mathbb{A}

.
We can write it as,

\begin{matrix} \displaystyle \mathbb{A}^T(\mathbb{Y} - \widehat{\mathbb{Y}})=0 \end{matrix}

Notice that

\mathbb{Y} - \widehat{\mathbb{Y}}

lives in

\((N(A^T))\)

The Left Null Space of matrix

\mathbb{A}

OR say

The Null Space of

\mathbb{A}^T

And Null Space of

\mathbb{A}^T

is perpendicular to the column space of

\mathbb{A}

So $\mathbb{Y} - \widehat{\mathbb{Y}}$ is perpendicular to the column space of $\mathbb{A}$ .

\mathbb{A}^T(\mathbb{Y} - \widehat{\mathbb{Y}})=0

and

\widehat{\mathbb{Y}}=\mathbb{A}\widehat{\mathbb{X}}

\Rightarrow \mathbb{A}^T(\mathbb{Y} - \mathbb{A}\widehat{\mathbb{X}})=0

\Rightarrow \mathbb{A}^T \mathbb{Y} - \mathbb{A}^T\mathbb{A}\widehat{\mathbb{X}}=0

\Rightarrow \mathbb{A}^T\mathbb{A}\widehat{\mathbb{X}}=\mathbb{A}^T \mathbb{Y}

\begin{matrix} \displaystyle \widehat{\mathbb{X}}=\left(\mathbb{A}^T\mathbb{A}\right)^{-1}\mathbb{A}^T \mathbb{Y} \end{matrix}

Our projection of

\mathbb{Y}

on the columnn space of

\mathbb{A}

\widehat{\mathbb{Y}}

\widehat{\mathbb{Y}}=\mathbb{A}\widehat{\mathbb{X}}

and

\widehat{\mathbb{X}}=(\mathbb{A}^T\mathbb{A})^{-1}\mathbb{A}^T \mathbb{Y}

, so

Projection

(\widehat{\mathbb{Y}})

\mathbb{Y}

on the column space of

\mathbb{A}

\begin{matrix} \displaystyle \widehat{\mathbb{Y}}=\mathbb{A}\left(\mathbb{A}^T\mathbb{A}\right)^{-1}\mathbb{A}^T \mathbb{Y} \end{matrix}

So our Projection Matrix is,

\begin{matrix} \displaystyle P=\mathbb{A}\left(\mathbb{A}^T\mathbb{A}\right)^{-1}\mathbb{A}^T \end{matrix}

\(P\)

symmetric?

\displaystyle P= \mathbb{A}(\mathbb{A}^T\mathbb{A})^{-1}\mathbb{A}^T

\displaystyle \Rightarrow P^T = \left(\mathbb{A}(\mathbb{A}^T\mathbb{A})^{-1}\mathbb{A}^T\right)^T

\displaystyle \Rightarrow P^T = \mathbb{A}^{T^T}((\mathbb{A}^T\mathbb{A})^{-1})^T\mathbb{A}^T

\displaystyle \Rightarrow P^T = \mathbb{A}^{T^T}\left((\mathbb{A}^T\mathbb{A})^T\right)^{-1}\mathbb{A}^T

\displaystyle \Rightarrow P^T = \mathbb{A}^{T^T}(\mathbb{A}^T\mathbb{A}^{T^T})^{-1}\mathbb{A}^T

\displaystyle \Rightarrow P^T = \mathbb{A}(\mathbb{A}^T\mathbb{A})^{-1}\mathbb{A}^T

\(P\)

is symmetric.

$\[P=P^T\]$

What if we project vector

\mathbb{Y}

on the column space of a matrix

\mathbb{A}

of a matrix

\mathbb{A}

twice?

When we apply the projection first time, we land in the column space of

\mathbb{A}

.
Let's say the projected vector be

\widehat{\mathbb{Y}}

.
If we again project the

\widehat{\mathbb{Y}}

on the column space of

\mathbb{A}

then the resultant vector will be

\widehat{\mathbb{Y}}

.
Because

\widehat{\mathbb{Y}}

is already in column space of

\mathbb{A}

, so the second projection did nothing.
So we can say that

$\[P^2=P\]$

Let's look at the extreme cases,
Suppose we want to take projection of a vector

\vec{b}

in the column space of a matrix

\mathbb{A}

\(1.\)

What If the vector $\vec{b}$ is perpendicular to the column space of matrix $\mathbb{A}$ ?

First let's think about the space of vectors who are perpendicular to the column space of matrix

\mathbb{A}

.
Space perpendicular to the column space is Null space of

\mathbb{A}^T

.
So

\vec{b}

lives in the Null space of

\mathbb{A}^T

.
So,

$\mathbb{A}^T\vec{b}=\vec{0}$

projection matrix

\((P)\)

of the column space of a matrix

\mathbb{A}

is,

$P= \mathbb{A}(\mathbb{A}^T\mathbb{A})^{-1}\mathbb{A}^T$

And projection

\(P\)

\vec{b}

in the column space of a matrix

\mathbb{A}

P\vec{b}

P\vec{b}= \mathbb{A}(\mathbb{A}^T\mathbb{A})^{-1}\underbrace{\mathbb{A}^T\vec{b}}_{=\vec{0}}=\vec{0}

\(2.\)

What If the vector $\vec{b}$ is in the column space of $m\times n$ matrix $\mathbb{A}$ ?

Vectors in the column space of

\mathbb{A}

is the linear combinations of the column vectors of matrix

\mathbb{A}

.
We can write the all the linear combinations of matrix all as

\mathbb{A}\vec{x};\quad\vec{x}\in\mathbb{R}^n

.
And we are saying that

\vec{b}

is in the column space of matrix

\mathbb{A}

, so ,

$\vec{b}=\mathbb{A}\vec{x};\quad\vec{x}\in\mathbb{R}^n$ .

So projection

\(P\)

\vec{b}

in the column space of a matrix

\mathbb{A}

P\vec{b}

P\vec{b}= \mathbb{A}(\mathbb{A}^T\mathbb{A})^{-1}\mathbb{A}^T\vec{b}

P\vec{b}= \mathbb{A}\underbrace{(\mathbb{A}^T\mathbb{A})^{-1}\mathbb{A}^T\mathbb{A}}_{\mathcal{I}( identity)}\vec{x}

P\vec{b}= \mathbb{A}\vec{x}

P\vec{b}= \vec{b}

.
So projecting

\vec{b}

(which is already in the column space of

\mathbb{A}

) on the the column space of

\mathbb{A}

changes nothing.