Column space

We discussed that a space is a vector space, if all linear combination of vectors (that are inside that space) lies in that space.
But what is this Column space? We know what is space, but what we meant by Column?
Here Column is referring to Column of a matrix.

Example in $\mathbb{R}^3$

Consider a matrix

A=\begin{bmatrix} 1 & 2\\ 1 & 3\\ 5 & 1\\ \end{bmatrix}

here each column is considered as a vector.
Matrix

\(A\)

has

\(2\)

columns so we have

\(2\)

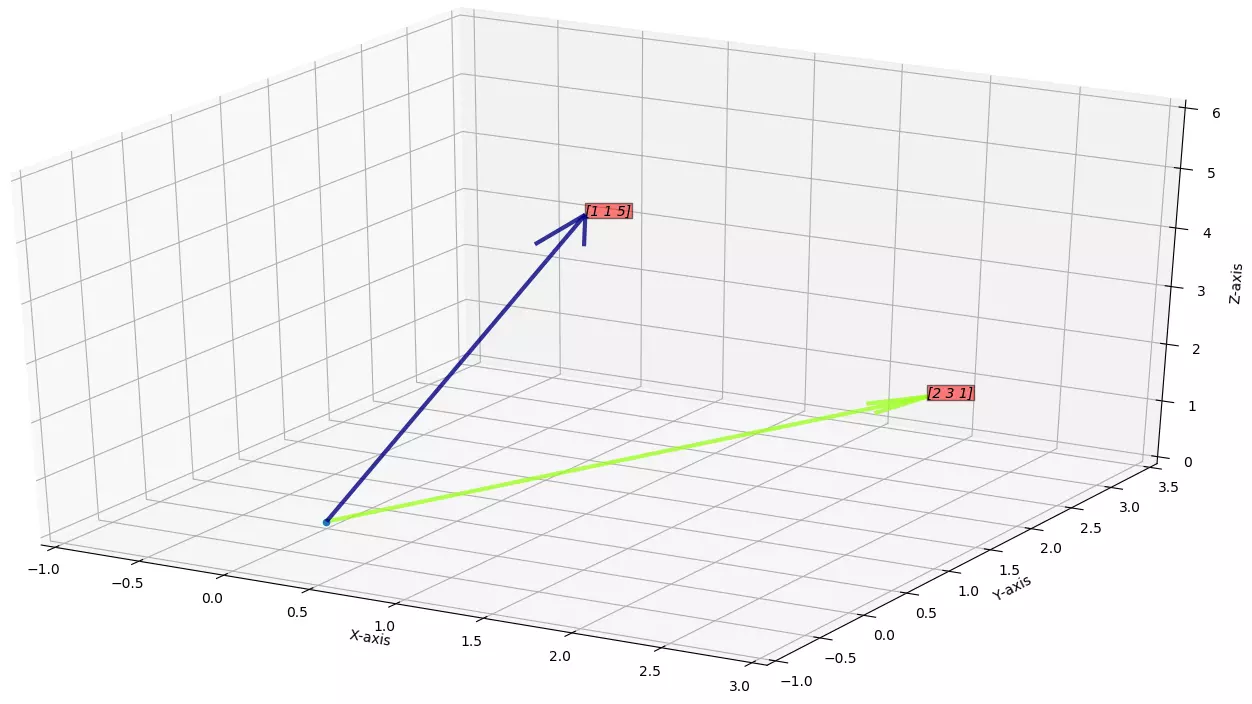
vectors, say

\vec{u}= \begin{bmatrix} 1\\1\\5\\ \end{bmatrix}\in\mathbb{R}^3;\quad

\vec{v}= \begin{bmatrix} 2\\3\\1\\ \end{bmatrix}\in\mathbb{R}^3;\quad

So we have

2\quad

\(3\)

-dimensional vectors.
So

Column space of matrix $$A$$ is defined by the vector space of these vectors $\vec{u},\vec{v}$ and vector space of $\vec{u},\vec{v}$ is all the linear combinations of vectors $\vec{u}$ and $\vec{v}$ .

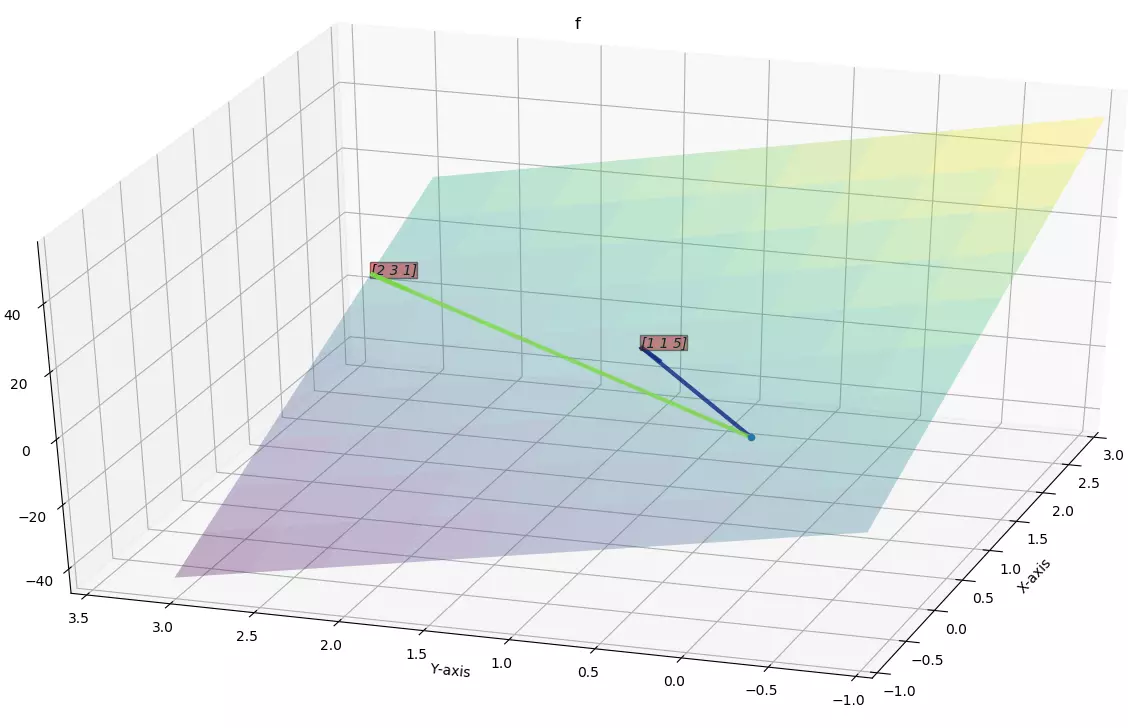
How does that vector space look like?

Here we can see $\vec{u}$ and $\vec{v}$ are non-parallel vectors so vector space of $\vec{u}$ and $\vec{v}$ is a plane.

Equation of plane

General equation of plane is

\(ax+by+cz+d=0\)

we know this plane passes through origin so

\(d=0\)

, and

\lt a,b,c \gt

is normal to plane which we can get by taking cross product between

\vec{v}

and

\vec{u}

\vec{u}\times\vec{v} = \lt -14,9,1 \gt

so equation of plane is,

\(-14x+9y+z=0\)

Code To plot this (python)

import MultiVariable as mvar
import numpy as np
%matplotlib qt
def f(x,y):
    return 14*x - 9*y

m = mvar.MultiVariable(count=10, x_range=(-1,3), y_range=(-1,3))
vectors = np.array([
                    [1,1,5],
                    [2,3,1],
                   ])
origin = np.array([0,0,0])
m.plot_3D_vectors(vectors, origin, plot_separately=False)
m.plot_surface_color_3D(f,plot_separately=False, alpha=0.3)
m.setX_limit((-1,3))
m.setY_limit((-1,3.5))

Download MultiVariable class

Example in $\mathbb{R}^4$

Consider a matrix

A=\begin{bmatrix} 1 & 1 & 2\\ 2 & 4 & 6\\ 3 & 6 & 9\\ 4 & 8 & 12\\ \end{bmatrix}

here each column is considered as a vector.
Matrix

\(A\)

has

\(3\)

columns so we have

\(3\)

vectors, say

\vec{u}= \begin{bmatrix} 1\\2\\3\\4\\ \end{bmatrix}\in\mathbb{R}^4;\quad

\vec{v}= \begin{bmatrix} 1\\4\\6\\8\\ \end{bmatrix}\in\mathbb{R}^4;\quad

\vec{w}= \begin{bmatrix} 2\\6\\9\\12\\ \end{bmatrix}\in\mathbb{R}^4

So we have

3\quad

\(4\)

-dimensional vectors.
So

Column space of matrix $$A$$ is defined by the vector space of these vectors $\vec{u},\vec{v},\vec{w}$ and vector space of $\vec{u},\vec{v},\vec{w}$ is all the linear combinations of vectors $\vec{u},\vec{v}$ and $\vec{w}$ .

How does that vector space look like?

Does it fill the whole

\(4\)

-dimensional space?

We have

\(3\)

vectors in

\mathbb{R}^4

and we can't fill a

\(4\)

dimensional space with just

\(3\)

vectors, doesn't matter how they are oriented.
So the answer is No

Does it fill a

\(3\)

-dimensional space?

Here you can see that

\vec{w}=\vec{u}+\vec{v}

, so

\vec{w}

lives in vector space of

\vec{u}

and

\vec{v}

So in total we have just

\(2\)

vectors

\vec{u}

and

\vec{v}

and we can't fill a

\(3\)

dimensional space with just 2 vectors, we at least need

\(3\)

(non-parallel) vectors to fill a

\(3\)

-dimensional space.
So answer is No

Does it fill a

\(2\)

-dimensional space?

Here you can see that

\vec{w}=\vec{u}+\vec{v}

, so

\vec{w}

lives in vector space of

\vec{u}

and

\vec{v}

, and,

\vec{u}

and

\vec{v}

are non-parallel vectors so vector space of

\vec{u}

and

\vec{v}

is a plane.
Combined all of that vector space of

\vec{u}

\vec{v}

and

\vec{w}

is a plane

\Rightarrow

Column space of matrix

\(A\)

is a plane.
So answer is Yes vector space of

\vec{u},\vec{v}

and

\vec{w}

fills a

\(2\)

-dimensional space?

Column space of a matrix $$A$$ is defined by all the linear combinations of it's column vectors.

Here we will denote the column space of matrix

\(A\)

\mathbf{C}(A)

Matrix Notation

We saw how we can find Column space using columns as vectors. Now let's find Column space of some matrix

\(A\)

in matrix notation.
Say we have a matrix

\(A\)

Now answer this,
Does $A\vec{x}=\vec{b}$ always have a solution for every $\vec{b}$ ?, and if the answer is No then which $\vec{b}$ do have a solution?
if

\(A\)

is a

n\times m

matrix, then

\vec{x}

is a

m\times 1

vector and

\vec{b}

n\times 1

vector.

Say our matrix is

A=\begin{bmatrix} 1 & 1 & 2\\ 2 & 4 & 6\\ 3 & 6 & 9\\ 4 & 8 & 12\\ \end{bmatrix}

then

\vec{x}=\begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ \end{bmatrix};\quad

x_i\in\mathbb{R}

and

\vec{b}=\begin{bmatrix} b_1 \\ b_2 \\ b_3 \\ b_4 \\ \end{bmatrix};\quad

b_i\in\mathbb{R}

Does

A\vec{x}=\vec{b}

always have a solution for every

\vec{b}

Here we have 3 variables

\(x_1,x_2,x_3\)

and 4 equations so, one of the

\(b_i\)

depends on one of

\(b_j\)

and

i\neq j

So we can't have solution for every

\vec{b}

, because of this dependency. So it rules out the possibility of

\(4\)

dimensional column space.
Because to be a Column space we must get every vector in that column space by the linear combinations of column vectors.

What are the

\vec{b}

that are possible?

A\vec{x}= \begin{bmatrix} 1 & 1 & 2\\ 2 & 4 & 6\\ 3 & 6 & 9\\ 4 & 8 & 12\\ \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ \end{bmatrix} = \begin{bmatrix} b_1 \\ b_2 \\ b_3 \\ b_4 \\ \end{bmatrix}

Ok we can't solve it for every

\vec{b}

but we can solve it for some

\vec{b}

.
For example:

For

\vec{b}=\begin{bmatrix} 1 \\ 2 \\ 3 \\ 4 \\ \end{bmatrix}

For

\vec{b}=\begin{bmatrix} 1 \\ 2 \\ 3 \\ 4 \\ \end{bmatrix} \quad

\vec{x}=\begin{bmatrix} 1 \\ 0\\ 0\\ \end{bmatrix}

A\vec{x}= \begin{bmatrix} 1 & 1 & 2\\ 2 & 4 & 6\\ 3 & 6 & 9\\ 4 & 8 & 12\\ \end{bmatrix} \begin{bmatrix} 1\\ 0\\ 0\\ \end{bmatrix} = \begin{bmatrix} 1\\ 2\\ 3\\ 4\\ \end{bmatrix}

For

\vec{b}=\begin{bmatrix} 1 \\ 4 \\ 6 \\ 8 \\ \end{bmatrix}

For

\vec{b}=\begin{bmatrix} 1 \\ 4 \\ 6 \\ 8 \\ \end{bmatrix} \quad

\vec{x}=\begin{bmatrix} 0 \\ 1\\ 0\\ \end{bmatrix}

A\vec{x}= \begin{bmatrix} 1 & 1 & 2\\ 2 & 4 & 6\\ 3 & 6 & 9\\ 4 & 8 & 12\\ \end{bmatrix} \begin{bmatrix} 0\\ 1\\ 0\\ \end{bmatrix} = \begin{bmatrix} 1\\ 4\\ 6\\ 8\\ \end{bmatrix}

Now you can see that the

\vec{b}

that can solve this system of equation is the

\vec{b}

that is in the column space of matrix

\(A\)

.
So

\vec{b}

is the linear combination of columns of matrix

\(A\)

Dependency

You can see that in our matrix

A=\begin{bmatrix} 1 & 1 & 2\\ 2 & 4 & 6\\ 3 & 6 & 9\\ 4 & 8 & 12\\ \end{bmatrix}

there is a column that we can get with linear combination of other columns.
(here I represent column

\(i\)

\(c_i\)

)

\(c_3=c_1+c_2\)

\(c_3\)

is in the vector space of

\(c_1\)

and

\(c_2\)

If we remove one of the column from matrix $$A$$ then the column space of matrix A will still be same.
say we drop column $$3$$ (We can drop column $$1$$ or column $$2$$ )
So say $A'=\begin{bmatrix} 1 & 1 \\ 2 & 4 \\ 3 & 6 \\ 4 & 8 \\ \end{bmatrix}$
Then $A'\vec{x}$ will also give all possible $\vec{b}$ that $A\vec{x}$ can.

So we can say that

Column space of $$A$$ and $$A'$$ are same, $\mathbf{C}(A) = \mathbf{C}(A')$

But we can't drop two columns from

\(A\)

because any two columns in our matrix

\(A\)

are independent of each other.
So we can say that Column space of matrix

\(A\)

is a

\(2\)

-dimensional subspace inside

\(4\)

-dimensional space.

Column space

Example in \(\mathbb{R}^3\)

Example in \(\mathbb{R}^4\)

Matrix Notation

Dependency

Example in $\mathbb{R}^3$

Example in $\mathbb{R}^4$